Kepler’s laws
Imagine taking a walk around your neighborhood. As you go, you notice that at certain points, you speed up – like when going downhill – and slow down in other spots. This change in pace might feel natural, even unnoticed, but it’s all about the environment you’re in. Believe it or not, a similar kind of journey happens in space, with planets orbiting the Sun. Instead of strolling around the block, they travel around in orbits, with some points being faster than others. It’s not just random; it’s governed by precise mathematical laws – Kepler’s Laws.
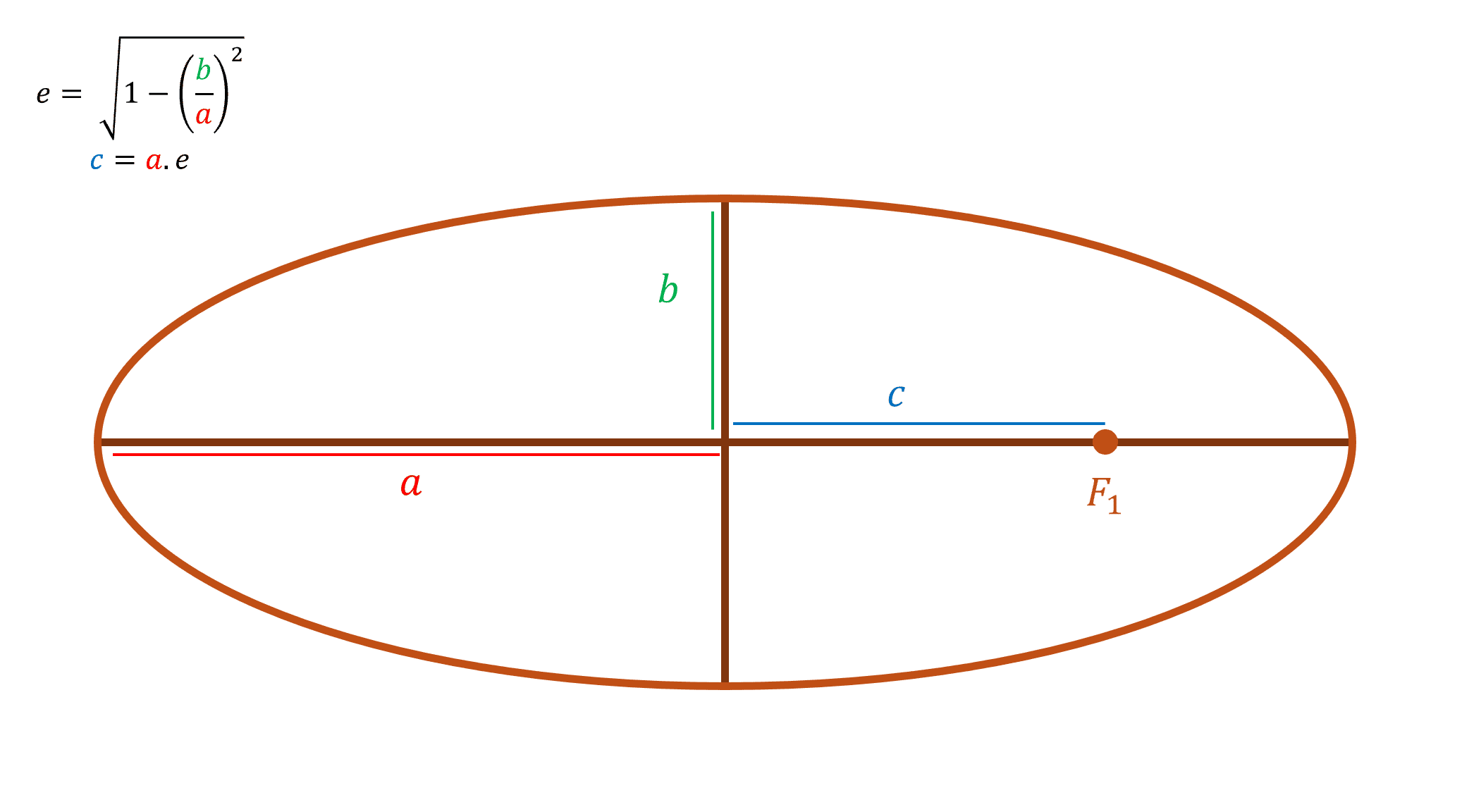
Kepler’s First Law: A Not-So-Perfect Circle
Think about the shape of a racetrack. It’s more of an oval, right? Planets do something similar. Kepler’s first law tells us that planets move in elliptical orbits, not perfect circles, with the Sun sitting at one of the foci. This was a huge revelation at the time because up until then, everyone thought orbits had to be perfect circles. Imagine setting a satellite in space to communicate with ships at sea. Its orbit around the Earth isn’t a perfect circle either, but an ellipse, meaning it gets closer and farther away at different points, which helps ensure it stays in just the right position for optimal coverage.
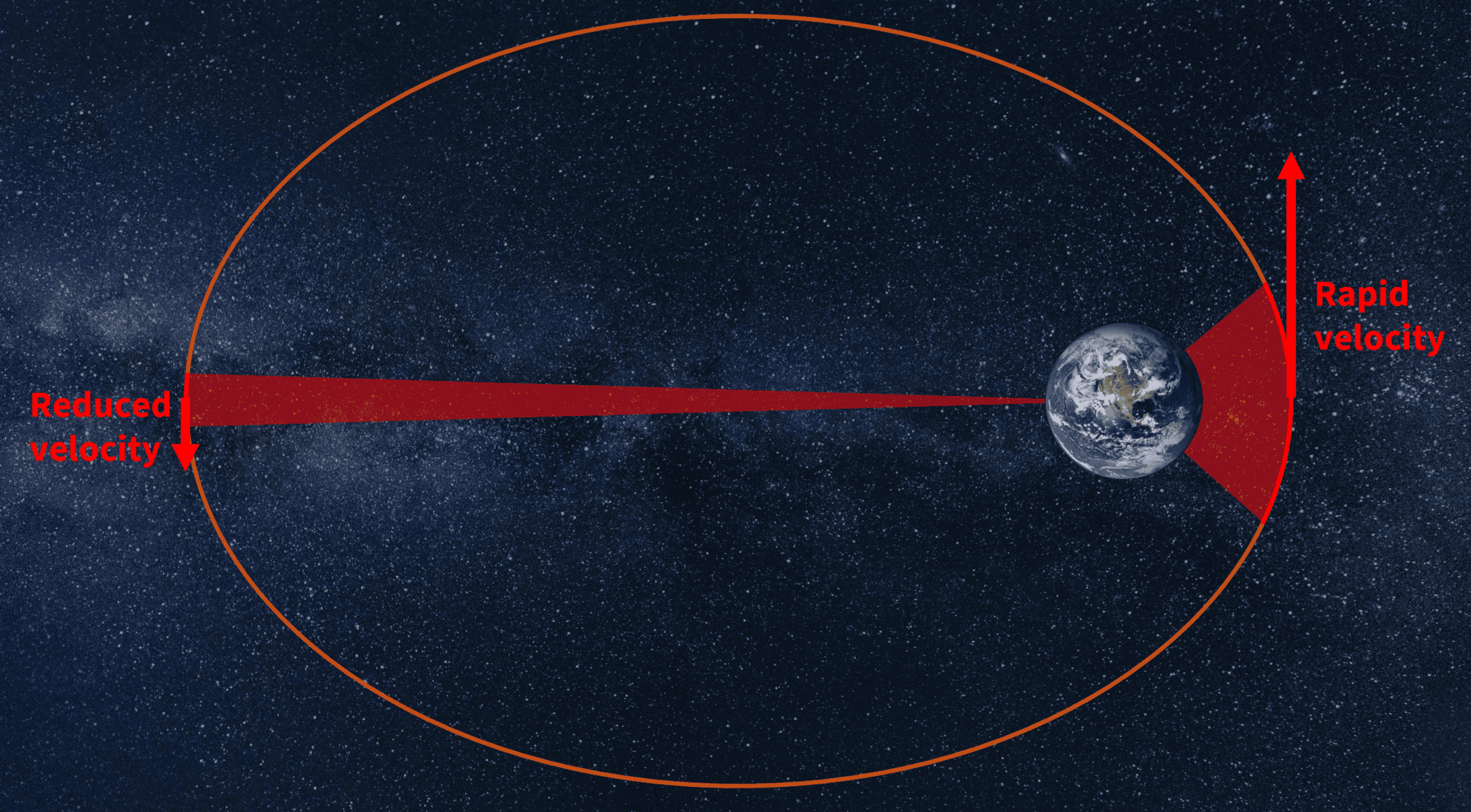
Kepler’s Second Law: Speeding Up and Slowing Down
Here’s where it gets interesting. Have you ever noticed that when you turn a corner while biking, you automatically speed up or slow down to navigate the curve? Kepler’s second law says that planets do the same thing. As they get closer to the Sun, they move faster, and as they move farther away, they slow down. This is because a line from the planet to the Sun sweeps out equal areas in equal times.
For instance, at Sternula, we use this same concept to ensure the right satellite coverage over the oceans. Our satellites adjust their velocities depending on their position in orbit, ensuring consistent maritime communications. Much like how a cyclist adjusts their speed to handle different terrains, satellites adapt their motion to maintain connection even in rough, unpredictable maritime conditions.
Where:
- A is the area in meter squared (m2)
- t is the time in second
- r is the radius of the orbit in meter
- θ is the anomaly angle in radian
- h is the angular momentum in kilogram meter squared per second (kg⋅m2/s)
- m is the mass in kilogram
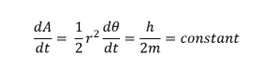

Kepler’s Third Law: The Farther Away, The Longer the Orbit
Ever had the experience of waiting for a friend who lives far away? You know that if they live close, it doesn’t take long for them to reach you, but if they live far, it takes much longer. Kepler’s third law explains a similar concept for planets. The farther a planet is from the Sun, the longer it takes to complete its orbit. This law helps scientists calculate the time it takes for objects, to orbit the Earth.
For satellite missions, this is crucial information. A satellite in a higher orbit will take longer to make one complete trip around the Earth, just like your friend taking longer to arrive from a faraway neighborhood.
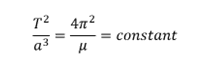
Where:
- T is the period of revolution in second
- a is the semi-major axis in meter
- µ = 3.986004418×1014 is the standard gravitational constant in meter cubed per second squared (m3/s2)
The Science Behind the Tech
Kepler’s laws, first formulated in the early 17th century, remain crucial for understanding not only planetary motion but also modern satellite technology. These laws explain how celestial bodies move in elliptical orbits, vary in speed depending on their distance from the central body, and how their orbital periods relate to their distance from the object they orbit.
In the realm of space science, Kepler’s insights have been applied far beyond the solar system. They underpin the placement and operation of satellites that support everything from GPS to global communications. Satellites, like planets, follow elliptical paths, and their velocity changes depending on their proximity to Earth. Understanding these motions helps engineers design precise orbits for various satellite applications, ensuring they provide uninterrupted services like navigation, telecommunications, and Earth observation.
Kepler’s laws provide the theoretical foundation that allows us to predict and optimize satellite trajectories, making space exploration and global connectivity possible today. In this way, the centuries-old discoveries of planetary motion continue to shape the cutting-edge technology that powers modern life.
Published on 08/11/2024, Written by: Cyriaque Guillot, Ivan Conti

